激活函数

概述

生物的神经网络激发了前人对人工神经网络的发展。激活函数（Activation function）是神经网络中一个至关重要的部分。

激活函数的存在是神经网络中用来添加非线性因素的，提升模型拟合的能力，如果没有激活函数，那么这个神经网络再深，也没办法去拟合任意函数。

所以我们使用的激活函数通常都是非线性的，因为如果使用线性的那么使用激活函数就没什么意义了。

神经网络用于实现复杂的函数，非线性激活函数可以使神经网络随意逼近复杂函数。没有激活函数带来的非线性，多层神经网络和单层无异。

神经网络单个神经元的基本结构由线性输出 Z 和非线性输出 A 两部分组成。如下图所示：

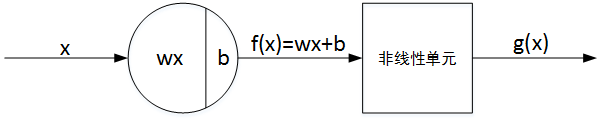
非线性激活函数

非线性激活函数有很多，是最常用的激活函数类型，非线性方程控制输入到输出映射。

非线性激活函数有：Sigmoid、Tanh、ReLU、Leaky ReLU、ELU、Maxout、PReLU、Swish、GELU等等等

本文只介绍几种常见的Sigmoid、Tanh、ReLU、Leaky ReLU和Parametric ReLU

Sigmoid

Sigmoid又叫作 Logistic 激活函数，函数的取值范围在 (0,1) 之间，单调连续，求导容易，一般用于二分类神经网络的输出层。该函数将大的负数转换成 0，将大的正数转换成 1。数学公式为：

$$\ \sigma(x) =\frac{1}{1+e^{-x}}$$

函数图像：

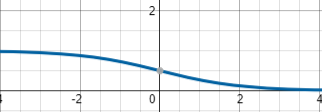
这里主要谈谈Sigmoid函数的缺陷：

• 梯度消失：Sigmoid 函数趋近 0 和 1 的时候变化率会变得平坦，也就是说，Sigmoid 的梯度趋近于 0。神经网络使用 Sigmoid 激活函数进行反向传播时，输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此，这些神经元的权重不会更新。此外，与此类神经元相连的神经元的权重也更新得很慢。该问题叫作梯度消失。因此，想象一下，如果一个大型神经网络包含 Sigmoid 神经元，而其中很多个都处于饱和状态，那么该网络无法执行反向传播。

---

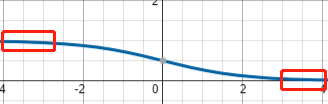
这里简单说一下梯度消失的问题

首先，再BP神经网络中，我们知道，我们想要更新一个特定的权重，更新规则为：

$$\ w_{new} = w_{old} - \mu \frac{\partial J_{total}}{\partial w_{old}}$$

但是如果我们的$\ \frac{\partial J_{total}}{\partial w_{old}}$过小，非常小，这时我们就遇到了梯度消失问题，其中许多权重和偏置只能收到非常小的更新。

我们假如$\ w_{old}$为0.2，最后更新到$\ w_{new}$为0.19999999999显然这个更新毫无意义，梯度很小，如同消失了一样，使得神经网络中的权重几乎没有更新。这会导致网络中的节点离其最优值相去甚远。

这个问题会严重妨碍神经网络的学习。

---

• 不以零为中心：Sigmoid 输出不以零为中心的。

---

这里也是有学问的，假如Sigmoid函数输出为$\ \sigma(Wx+b)$ 且满足$\ 0<\sigma (Wx+b) <1$

在反向求导的过程中，令损失函数$\ J$对$\sigma (Wx+b)$ 的求导为 $\ \sigma$ ，计算$\ J$对$\ W$的偏导数：

$$\ dW = d\sigma \cdot \frac{d}{dW}(\sigma(Wx+b)) = d\sigma \cdot \sigma(Wx+b)(1-\sigma(Wx+b))\cdot x$$

其中，$\ \sigma(Wx+b)>0, 1-\sigma(Wx+b)>0$

若神经元的输入 $\ x>0$，则无论 $\ d\sigma$ 正负如何，总能得到 $\ dW$ 恒为正或者恒为负。也就是说参数矩阵 $\ W$ 的每个元素都会朝着同一个方向变化，同为正或同为负。这对于神经网络训练是不利的，所有的 $\ W$ 都朝着同一符号方向变化会减小训练速度，增加模型训练时间。就好比我们下楼梯的所需的时间总比直接滑梯下来的时间要长得多，如下图所示：

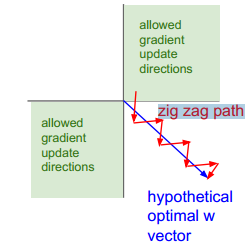
图中，红色折线是上文讨论的情况，蓝色斜线是 W 不全朝同一方向变化的情况。

值得一提的是，针对Sigmoid函数的这一问题，神经元的输入$\ x$常会做预处理，即将均值归一化到零值。这样也能有效避免$\ dW$恒为正或者恒为负。

---

• 计算成本高昂：exp()函数与其他非线性激活函数相比，计算成本高昂。

Tanh

公式为：

$$\ \frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}$$

函数图像为：

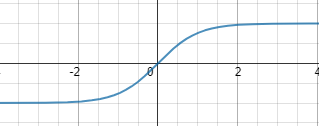
Tanh 激活函数又叫作双曲正切激活函数（hyperbolic tangent activation function）。与 Sigmoid 函数类似，Tanh 函数也使用真值，但 Tanh 函数将其压缩至-1 到 1 的区间内。与 Sigmoid 不同，Tanh 函数的输出以零为中心，因为区间在-1 到 1 之间。你可以将 Tanh 函数想象成两个 Sigmoid 函数放在一起。在实践中，Tanh 函数的使用优先性高于 Sigmoid 函数。负数输入被当作负值，零输入值的映射接近零，正数输入被当作正值。唯一的缺点是：

• Tanh 函数也会有梯度消失的问题，因此在饱和时也会“杀死”梯度。

ReLU

ReLU函数代表的的是“修正线性单元”，它是带有卷积图像的输入x的最大函数(x,o)。ReLU函数将矩阵x内所有负值都设为零，其余的值不变。

它的数学公式为：

$$\ f(x) = max(0,x)$$

函数图像为

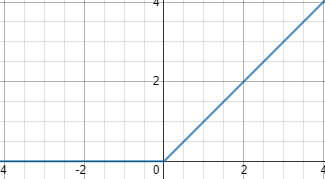
ReLU是最常用的一个激活函数，它没有饱和区，不存在梯度消失问题，没有复杂的指数运算，计算简单、效率提高，实际收敛速度较快，大约是 Sigmoid/tanh 的6倍，比 Sigmoid 更符合生物学神经激活机制。

但是ReLU函数也有一些缺陷：

• 不以零为中心：和 Sigmoid 激活函数类似，ReLU 函数的输出不以零为中心。

• 前向传导过程中，如果 x < 0，则神经元保持非激活状态，且在后向传导中“杀死”梯度，导致神经元“死亡”。这样权重无法得到更新，网络无法学习。当 x = 0 时，该点的梯度未定义，但是这个问题在实现中得到了解决，通过采用左侧或右侧的梯度的方式。

---

关于神经元“死亡”

用一个简单的神经网络举个例子

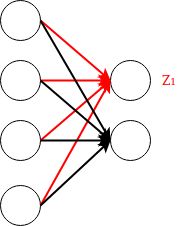
对于这个神经网络，$\ W$为2x4的矩阵，单个训练样本$\ x$为4x1的向量

所以：

$$\ z_1 = \left [ W_{11} \quad W_{21} \quad W_{31} \quad W_{41} \right ]\cdot\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\\x_{4}\end{bmatrix}$$

假设这个时候$\ W$坏掉了，对所有的训练样本$\ \vec{x}$，输出的这个$\ Z_1$始终是小于0的数，那么：

$$\ a_1 = ReLU(z_1) = max(z_1,0) = 0$$

所以激活函数的输出值永远都是0，回到反向传播：

$$\ \frac{\partial J}{\partial z_1} = \frac{\partial J}{\partial a_1}\frac{\partial a_1}{\partial z_1}$$

其中，由于$\ z_1<0$时，$\ a_1 = 0$ 。所有$\ \frac{\partial a_1}{\partial z_1} = 0$恒成立

所以：

$$\ \frac{\partial J}{\partial z_1} = \frac{\partial J}{\partial a_1}\frac{\partial a_1}{\partial z_1} = \frac{\partial J}{\partial a_1}\cdot 0 = 0$$

所以：

$$\ \frac{\partial J}{\partial W} = \frac{\partial J}{\partial z_1}\cdot x^T$$

所以$\ \frac{\partial L}{\partial W} = \vec{0}^T$恒成立

---

Leaky ReLU

公式：

$$\ max(0.1x,x)$$

函数图像：

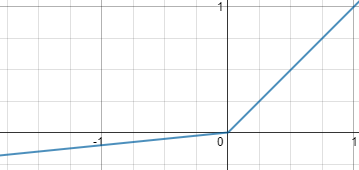
Leaky ReLU 的概念是：

当$\ x < 0$时，它得到0.1的正梯度。该函数一定程度上缓解了ReLU中的死亡神经元的问题，但是使用该函数的结果并不连贯。它具备ReLU激活函数的所有特征，如计算高效、快速收敛、在正区域内不会饱和。

Parametric ReLU

PReLU 函数的数学公式为：

$$\ f(x) = max(\alpha x,x)$$

其中$\ \alpha$是超参数。这里引入了一个随机的超参数，它可以被学习，因为你可以对它进行反向传播。这使神经元能够选择负区域最好的梯度，有了这种能力，它们可以变成 ReLU 或 Leaky ReLU。